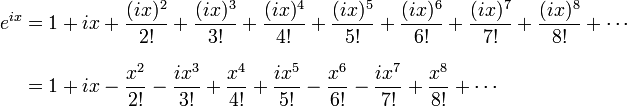Rovers

guscostLeave a comment

Here’s an interesting idea from John Graham-Cumming suggesting that “Rovers” like Curiosity could be useful in other environments. Specifically, the Earth is a gigantic place and most of it is hard for humans to access. Why don’t we have Earth Rovers that can perform simple tasks in those places?

I can see why having surveillance equipment in remote locations might make people nervous, because people generally don’t like being watched. This makes sense, but it completely ignores all of the other cases where “roving” can be helpful. Security is only one thing that computers do well, and we can learn a great deal by not judging what we see until we have a better picture. Sometimes waiting for an answer is the best thing to do.

Why I Pay for a Social Network or: The Money Really Is a Red Herring

guscost2 Comments

Interestingly, and almost right on cue, the free police have descended on Dalton Caldwell for following through with something as original and outside-the-box as his audacious proposal, the supremely interesting app.net alpha community (and associated API). These doubters are mostly, I don’t know, anti-technology-business-experiments or something, and I’ve decided that they simply do not understand its significance yet.

If I may hazard a guess, what these late adopters aren’t grasping is the fact that right now, app.net is a lot more expensive than the sticker price seems to suggest. The cheaper options are still closer to $1000 on the cost side for I’d say the dominant majority of its users. Do you know why? Most of them seem like they’re busy hustling some kind of profit that they can live off of, and even participating in this network, to say nothing of developing for it, is an enormous time investment! We’re putting our money down to give Dalton food and motivation, because he’s convinced us that 50 bucks a year does not matter anymore for a network with as much potential as this. I’d pay twice as much every year just for the publishing functionality, regardless of how many users stick around, and especially if they maintain this superb commitment to the product. Think about what you are actually using your money for, people! This is starting to look ridiculous – I think it’s rather undeniable that Dalton has touched one heck of a nerve here!

There is only one way that the app.net community can ever shake off the rather myopic “elitist Twitter” label that naysayers seem to be gravitating towards, and start something that I think a lot of people around the world will want. That is to prove to them what a network of interested parties can do. To that effect, I’m working on a new Chrome extension called AppAnnotate that uses the app.net API to let people annotate any web page and share notes with friends. The way of the future!

Degrees and Freedom

guscost4 Comments

Here’s my idea of a good math lesson. I want to explain Euler’s formula, the cornerstone of multidimensional mathematics, and one of the truly beautiful ideas from history. In school this formula appears as a useful trick, and is not commonly understood. I think that is because students are denied enough time to wonder what the formula actually means (it doesn’t describe how to pass an exam). Here is Euler’s formula:

e^(ix) = cos(x) + i*sin(x)

This idea was introduced to me after a review of imaginary and complex numbers. Once the history and definition were out of the way, we completely freaked out at the idea of putting ‘i’ in the exponent, then practiced how to use it in calculations. I might have had a brief moment of clarity in that first class, but by the AP exam Euler’s formula was nothing more than a black box for converting rectangular coordinates to polar coordinates.

Many years later, I came across the introduction to complex numbers from Feynman’s Lectures on Physics, and suddenly the whole concept clicked in a way that it never had in school. Explained here, I don’t think it is really that difficult to understand, but then I’ve already managed to understand it, so I’ll try to communicate my understanding and then you can tell me whether it makes sense.

We need to start by generalizing the concept of a numeric parameter. The number line from grade school is an obvious way to represent a system with one numeric parameter. If we label the integers along this line, each mark corresponds to a grouping of whole, countable things, and the value of our integer parameter must refer to one of these marks. If we imagine a similar system where our parameter can “slide” continuously from one integer to the next, the values that we can represent are now uncountable (start counting the numbers between 0.001 and 0.002 if you don’t believe me) but opening up this unlimited number of in-between values allows us to model continuous systems that are much harder to represent with chunks.

Each system has a single numeric parameter, even though the continuous floating-point parameter can represent numbers that the integer parameter cannot. In physics, the continuous parameter can represent what is called a “degree of freedom,” basically a quantity that changes independently of every other quantity describing the system. Sometimes a “degree of freedom” is just like one of the three dimensions that you can see right… now, but this is not always the case. Wavefunctions in particle physics can have infinite degrees of freedom, even though the objects described by these esoteric equations follow different laws when we limit our models to the four parameters of spacetime.

Anyway, the imaginary unit or ‘i’ is just some different unit that identifies a second numeric parameter. If we multiply an integer by ‘i’, we’re basically moving a second parameter along its own number line that same distance. Apply the “sliding” logic from before and we can use the fractional parts between each imaginary interval. If this sounds new and confusing, just remember that any “real” number is itself multiplied by the real unit, 1. Personally, I don’t think that the word “imaginary” should be used to describe any kind of number, because all numbers are obviously imaginary. However, this convention exists regardless of how I feel about it, and nobody would know what to put in Google if I used a different word.

Why do teachers use this system where one implicit unit is supplemented by a second explicit unit? Simple – it was added long before anyone fully understood what was going on. The imaginary unit was the invented answer to a question, that question being:

Which number yields -1 when multiplied by itself?

The first people to ask this question didn’t get much further than “A number called ‘i’ which is nowhere on the number line, and therefore imaginary.” If those scholars had described their problem and its solution in a different way, they might have realized some important things. First, this question starts with the multiplicative identity (1) and really asks “which number can we multiply 1 by twice, leaving -1?” Thinking about it like this, it soon becomes clear that the range of values we can leave behind after multiplying 1 by another value on the same number line, twice, cannot include -1! We can make 1 bigger, twice, by multiplying it by a larger integer, or smaller, by multiplying it by a value between 0 and 1. We can also negate 1 twice while scaling it up or down, but none of these options allow for a negative result!

A clever student might point out that this is a stupid answer and that we might as well say there is none, but we still learn about it because amazing things happen if we assume that some kind of ‘i’ exists. We can imagine a horizontal number line, and then a second number line going straight up at 90° (τ/4 radians, a quarter turn) from the first. Moving a point along one line won’t affect its value on the other line, so we can say that the value of our ‘i’ parameter is represented on the vertical line and the value of our first (“real”) parameter is represented on the horizontal line. That is, a complex number (a*1+b*i) imagined as a single point on a 2-dimensional plane. In this space, purely “real” or purely “imaginary” numbers behave just like complex numbers with zero for the value of one parameter.

Now think about the answer to that question again. If our candidate is ‘i’ or some value up “above” the real number line, it’s easy to imagine a vector transformation (which we assume still works like multiplication) that can change 1 to ‘i’ and then ‘i’ to -1 in this 2D number space. Just rotate the point around the origin by 90°. When our parameters are independent like this, exponentiation by some number of ‘i’ units is exactly like rotating the imagined “point” a quarter turn around zero some number of times. I don’t really know why it works, but it works perfectly!

We’ve seen that imaginary units simply measure a second parameter, and how this intuitively meshes with plane geometry. Now let’s review what is actually going on. Numbers multiplied by ‘i’ behave almost exactly like numbers multiplied by 1, but the important thing about all ‘i’ numbers is that they are different from all non-‘i’ numbers and therefore can’t be meaningfully added into them. The ‘i’ parameter is a free parameter in the two-parameter system that is every complex number. It can get bigger or smaller without affecting the other parameter.

Bringing this all together, let’s try to understand what Euler was thinking when he wrote down his formula, and why it was such a smashing success. He noticed that the Taylor series definition of the exponential function:

Exponential function and its Taylor series

Becomes this:
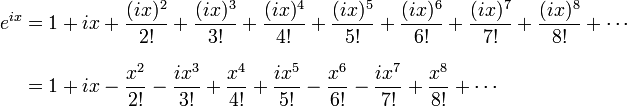
Complex exponential and its Taylor series

When ‘i*x’ is the exponent, because the integer powers of ‘i’ go round our complex circle from 1 to i to -1 to -i and back. Grouping the real terms and the ‘i’ terms together suddenly and unexpectedly reveals perfect Taylor series expansions of the cosine and sine:
Euler's complex exponential series

As each expansion is multiplied by a different free parameter, the two expansions don’t add together, naturally separating the right side of our equation into circular functions! We can just conclude that those functions really are the cosine and sine of our variable, remembering that the sine is an ‘i’ parameter, and it works! Because these expressions are equivalent, having a variable in the exponent allows us to multiply our real base by ‘i’ any fractional number of times (review your exponentials), and thus rotate to any point in the imagined complex plane. There are other ways to prove this formula, but I still do not understand exactly why any of the proofs happen the way they do. It’s not really a problem, because Euler probably didn’t understand it either, but I’d still like to come across a good answer someday. What I know right now is that any complex number can be encoded as a real number rotated around zero by an imaginary exponent:

e^(ix) = cos(x) + i*sin(x)

Here is proof that certain systems of two variables can be represented by other systems of one complex variable in a different form, and the math still works! Euler’s formula is a monumental, paradigm-shattering shortcut, and it made the modern world possible. I’m not overstating that point at all, everything from your TV to the Mars rover takes advantage of this trick.

Advertising

guscostLeave a comment

This new iOS project is essentially an experiment in direct-selling digital goods, so I’m not especially hung up on all these gnarly new questions about ads and their value, on Google and Facebook but offline as well. Yet it would be very wrong to assume that I can disregard business stuff like ad-based marketing, because ideas like MixBall will always need the attention and support of customers or fans or patrons or investors, and now that I’m pondering unanswered questions about promotion and consumer behavior, here are some random weekend advertising ideas:

– Why is the sound always overcompressed in video commercials? I mute the stream and therefore this does not seem to have the effect that the producers are intending. The only explanation I can imagine is that a lot of people walk into the next room or have a chat during commercial breaks, and either the proportion of those people is greater than the proportion of people who get annoyed by obnoxious audio quirks, or those people spend more money on advertised goods.

– I guess the colors are usually all blown out too, does that annoy visual people? Should sponsors care about this stuff?

– Can advertising work? Of course. Does most advertising work? Very different question…

– I’m not that nervous about Facebook spying on and then advertising to me based on my personal life (maybe I should be), but aren’t they something like 50 years behind with this idea that canned social advertising can convince me to spend where a straight commercial would fail? Isn’t it already uncool to buy the same stuff as the other people that I know?

– Is anyone else annoyed when ads and media have that obvious sort of glossy, meatless focus-group quality to them? Rows of brilliant-white, picket-fence teeth sparkling from inside diverse and demographically-precise protagonists, an awkward and asinine cliche grafted here, an agreeable slice of the Generic American Songbook cued there, and I slip right right into “uncanny valley” mode. It bothers me more than the hypothetical NSA archive of my Facebook timeline, because it feels vaguely as if the culture I belong to is being imitated by an alien entity in camouflage. I stare at this grotesque parody of human interaction, and my animal brain recoils at the knowledge that it is about to be tempted with yet another inappropriate way to spend money. Needless to say, the experience does not put me in a buying mood. The worst offenders of this kind seem to be movie previews, and I can’t tell if the effect is actually more noticeable these days, or if I’m just more likely to perceive it after brief exposure to film school. How can advertisers prevent this problem, and again, would they even want to?

– I’m thinking mostly about video ads, even specifically the kind that pop up for a mandatory 30-second interruption. Does anything else work, online? Do unexpected things work with small and/or weird subsets of the population? I suppose market researchers have answered many of those questions already, and I could probably buy access to some of the answers.

– Does that information matter for every product? Is anything more effective than a personal recommendation? Does anything else even come close?

MixBall Preview

guscost2 Comments

It’s about time to take the wraps off my latest project:

Introducing MixBall, the first dedicated interactive music platform! Tilt your iDevice to control how the music unfolds, and don’t hit any hazards if you want to survive all the way to the end! It gets rather difficult once all 3 tracks are in play…

Check out the sample video, and visit mixball.com to get on the mailing list. I’ll be sending out an update as soon as MixBall is available in the App Store!

Content

guscost1 Comment

I’m obsessed with content lately, because on average, its value seems to be falling as fast as the cost of production and distribution technology. I’m incredibly excited that the barrier to entry for an independent musician has never been lower than it is right now, for example, but this situation is causing other problems. Promotion is now far and away the largest investment that a typical media producer has to make, so quality suffers. And because fans now have essentially unlimited access to content, they are becoming jaded to the considerable effort that still goes into actually creating it, and are less willing to give their money to media producers as a result.

Those who believe that content curators don’t actually need to own and care for their music, or books, or videos, or software (or that the Internet can conjure up all of these things and more, indefinitely, by virtue of its very existence) will eventually realize what happens when an algorithm or a social phenomenon is trusted to organize and archive ideas. Specifically, it still does not work very well.

The “Netflix problem” is a good example: I can access a massive library of motion media at any time, bought from established studios and streamed through the Internet to my TV, and yet almost every time I simply want to pick out a movie to watch, I can never find it on Netflix. If I always knew that I was going to be interested in “mind-bending foreign thrillers” or maybe “goofy critically-acclaimed comedies” then I would have much less of a problem finding appropriate content, but that is never what I am actually looking for. In general, when I take the time to watch a movie, I want to see ideas that are important, and useful, and novel, and skillfully presented. Basically, I want to see the “good” movies by my own definition of “good,” and Netflix doesn’t provide more than 10 mediocre recommendations in that category.

Of course it really couldn’t be any other way, because scientifically, the whole Internet is just a bunch of smartass humans who wired their computers together for efficiency! More people need to understand that idea. I see a lot of what I’d almost call disappointment, because Facebook wasn’t actually able to save the Middle East, or because the next Instagram will sell for a lot less than a billion dollars, or because Justin Bieber is still famous, and it doesn’t really sit right with me at all. In fact, it seems rather naive and entitled.

Although the ponzi schemers may say otherwise, there has never been any magical voodoo behind this Internet business. Even if there was, Newton and Maxwell never could have done Einstein’s work by crowdsourcing it. The Internet only matters because the people who built it and use it have done great things with it. It will never be great or profitable or world-changing for any other reason.

St. Jobs

guscostLeave a comment

I’m sure there will be glowing biographies about Steve Jobs and his many accomplishments in time, but that guy deserves every single bit of the massive praise that is heaped upon him. Some of the most interesting comments come from the journalist disciples who all but compare Jobs to Jesus at every opportunity, and from the corresponding messiah-doubters who say that Jobs was nothing more than a savvy businessman who understood timing, manufacturing and product placement. However, other contrarians are understandably uncomfortable with his role in the commercialization of independent software and his control over the iUniverse, like a charismatic sort of software dictator type figure. Many of these people have Apple on their “modern hypocrites list” and might tell you so if the conversation wanders in that direction.

Here’s maybe the one valid way I could compare Steve Jobs to Jesus: Jesus was all about ideas that could outlast and defeat humans, no matter how powerful they might seem at the time. Steve made computers and computer systems that will outlast their owners. I can’t possibly imagine a day when my iPad (2) is any less useful or amazing than it is today unless it smashes, no matter what the next ten versions look like. We are going to have to explain to our kids that this is a weird new thing! Computers used to be rickety, noisy boxes with all these wires and different parts sticking out everywhere, and they used to break all the time when a competent engineer wasn’t available to keep things working! All you early majority consumers of a certain influential desktop operating system know exactly what I am talking about…

Somewhat ridiculously, the very approach that allowed Steve and Apple to end this massive problem with casual computing was his uncompromising, even autocratic management of the platform. It feels like I might be stepping on the dreams of the free and open software communities a bit here, but I think I’m starting to understand the actual logic in favor of Apple’s paradoxical mecha-fascism, if only because I program sounds and other fast things. Not every computer has the luxury of being some genius freedom-fighter’s personal data management device. Many computers have to control cars, and medical machines, and all those other things that can’t break or otherwise present an end user with some unpredictable software issue that needs debugging. When my grandma is trying to call me on video chat, it has to be the same way. That was his reasoning, I think, and I have to agree that it makes a lot more sense than it used to.

One day, when we’re donating these old tablets to needy kids or whoever, we might remember Steve by understanding what he wanted to create: a world united by its magical and powerful technology – technology we can use to do formerly impossible things, without losing all of our time in the process.

What is Art?

guscost2 Comments

Art is not about overpriced images, inaccessible music, or boring film. The general concept, which has no useful word, describes efficient communication, where in every case the artist has managed to fit some “large” idea into a comparatively “small” package for distribution. If a given thing is to be called “Art” then this efficiency must exist in some sense. However, no objective standard can determine whether a candidate message is “efficient enough” to qualify. As with comedy, each individual might arrive at a different answer to that question, depending on which new and useful ideas are communicated to and understood by that individual.

Reality should not anger creative people or create conflict between them, but alas, it is sometimes ignored by “Artists” busy in denial about the long-term sustainability of their ideas. These creatures have never sought efficient communication, instead occupying themselves with the construction of a grand strategic agreement bubble, in which obscurity or inaccessibility to anyone outside the bubble is painstakingly interpreted as an ideal outcome. I suspect their logic goes something like this: Because other smart people behave like my Art means something to them, my Art must mean something to the universe. If anyone behaves like my Art means nothing to them, they must be stupid and wrong.

This insular, counterproductive attitude seems to grow within a creative community as a new medium goes mainstream and the associated production industry matures, evidenced by the fact that painters and poets live in the most oppressive bubbles of all, while filmmakers and programmers have only recently arrived and started to network with The Machine (historically speaking). Politics infect everything, revenue becomes the new quality, and the real creators who decide to stay with their craft are neglected and abused.

One can only hope that this regrettable outcome is not inevitable, or even that it is a relic of capitalism, mass production and the necessary physicality of early distributed media. But a lot of people are still out there buying crap and calling it Art. Maybe that will be the case until they or we are all dead. It’s not very encouraging to people who produce ideas in exchange for anything other than money.

As artists, what can be done? Well, we can always rush into some unexplored, newfangled hi-tech medium, and try to keep the quality alive by virtue of diversity and evolution and all that. However, there is also no reason to think that the “old” media have been lost to the barbarians just yet. Great writers, painters, musicians, filmmakers, and other craftspeople are still out there, dreaming of amazing things that nobody has ever seen or heard or touched or tasted. Some will find ways to turn those dreams into reality. The only question is whether media producers acknowledge this reality, or die in some bubble.

Comedy

guscost1 Comment

Today I want to talk about comedy, because it is an absolutely amazing subject. The fact that an entire dynastic profession exists to make groups of (hopefully drunken) strangers laugh on command just seems kind of unbelievable. Clearly there is something deep and transformative about laughter, but what does it really mean when a person is compelled to laugh at something? For any aspiring jokesters out there, how can a comedian create this situation and get paid?

Well, in scientific terms, laughter is probably caused by something that behaves like a central pattern generator in the nervous system. These neural structures generate rhythmic output patterns without relying on any external feedback, so it is a bit strange to apply this concept to laughter (a person has to hear or see every joke, for example). However, the laughter usually happens only after a person gets the joke, at which point the “joke input” has ended in almost every case.

Therefore we should probably be conceptualizing laughter as an internal rhythmic feedback loop that can be started by some “funny” input. The challenge then is to define a “funny” input. I’ll pause for a second here so you can try that…

But wait! Doesn’t the very incomprehensibility of the challenge suggest something profound about how we should understand humor? Everyone knows that jokes are hard to write because an original comedian has to be the first person to notice that a certain thing is funny. The whole art of comedy revolves around having some of that uncommon and funny knowledge, and choosing to reveal it in the most entertaining way possible. Knowing this, is it possible to imagine something that all funny things must have in common?

Well, sure. They’re all “correct” in some abstract sense. Comedy is the process of being so profoundly correct that other people are compelled to laugh as soon as they realize what is going on. Us college-educated folk can scoff at low-brow humor, but almost any example of “bad” comedy still does reveal more than a few simple truths to more than a few tragically underinformed people, and therefore it can still make a lot of money. The fact that a thing is not funny to every person does not mean that it is not “funny” in some platonic sense. Somewhat disappointingly, there is no such thing. That makes good comedy very hard work, but at least we don’t ever have to fear the funniest joke in the world.

(From this perspective, slapstick humor is a special case where the truth being revealed is basically how badly it must suck for the victim…)

Generally speaking, this is not a new idea at all. A government document says this:

The American comedian Will Rogers was asked how he conceived his jokes. He answered: “I don’t make jokes. I just watch the government and report the facts.” See what I mean? Sometimes the truth is funnier than “comedy.”

Several Woody Allen bits are included as example one-liners, like this one:

I can’t listen to that much Wagner. I start getting the urge to conquer Poland.

It’s funny because it combines and reveals several truths in a clever and efficient way:

  • Wagner was a German imperialist.
  • Music conveys emotion.
  • Germany conquered Poland (and murdered millions of Jews) in World War II.
  • Woody Allen is Jewish.

The joke actually depends on the audience already knowing all of these things, and the “trick” is that he alludes to each in such an efficient and thought-provoking way, in the space of two short sentences. When we realize, all at once, the absurdity contained in the idea of a modern American Jew savoring hypnotic war hymns that ushered in the Second Reich, the effect is very funny for a lot of people, even if they don’t want to think about it!

I’m particularly interested in this method of “humor analysis” because it seems to emerge so naturally from a feedback-dominated model of intelligence. Laughter happens when a person notices something that is interpreted as “true enough” to activate an unconscious neural feedback loop, forcing them to externalize their acknowledgement and understanding. That is the sole evolutionary function of laughter, a phenomenon which almost certainly had a pivotal role in the building of every human civilization.

This is not saying that Adam Sandler is the greatest American ever, or even that we should all start studying Internet memes for the sake of science. But it does mean that we should take a moment and bow our heads in respect to every person who has ever wanted to make another person laugh, and in recognition of the great things they have accomplished for the sake of humanity. Because when a country of people stop what they are doing and start laughing (against their will) at the same idea at the same time, you can probably trust it a bit more than usual.

How would I define a “funny” thing? Funny things are true enough to make people laugh.

Here is someone else’s definition:

There is no simple answer to why something is funny… Something is funny because it captures a moment, it contains an element of simple truth, it is something that we have always known for eternity and yet are hearing it now out loud for the first time.

Notes from Silicon Valley

guscost2 Comments

As fun as this blog might be for me to write, and as many random ideas might play out (and succeed!) here, I still haven’t talked very much or very directly about myself or what I think about my own situation, as it didn’t really occur to me that certain people might care about that too. Family and friends, feel free to consider this The Return On Your Investment, Part 1, or whatever:

– The simulacres phenomenon is very real indeed. Humans may have bootstrapped their own existence all along, but moving to a place like this really underlines how far we’ve come as a species. I’m still not completely able to relax and enjoy myself when the ambient temperature is more than three degrees from whatever would seem “ideal” at any moment, because I have never known survival that does not require a carefully-constructed box. My ancestors fled nameless European tyrants in a box, and each subsequent generation of Northeastern Americans go on reproducing their boxes like some quasi-species of box-creature, just so that come springtime the whole lot of us aren’t frozen up in a giant cube. The problem is, boxes cut both ways, and people get soft. Like me.

– Maybe you think, ah, it must be that famous “crunchy” perspective from the camping trip, but this is not true either. Many people here seem to know their environment better than they know themselves. Some would not even regard that kind of statement as an insult.*

– Ever talk to one of those people who are too clever for their own good? Where we should probably just stuff them in the nearest closet or mental institution for a few hundred years while everyone else grows up? You’ll run into a lot of those people here.

– On the other hand, we have a verifiable shortage of free lunches, as people keep asking me to replace theirs. Actually, I did get a free lunch last week, but of course there was a waiting list involved. And the best free food is still reserved for the best free programmers, somehow.

– If I am willing to deal in money, there are many lunches available for purchase, most of which are delicious.

– As delicious as the marine life might be, Italian Food in City X doesn’t hold a candle to the real thing. Which, of course, doesn’t hold a candle to the real thing.

– No matter what happens, the hipsters have no choice but to become old with me.

– In the end, nothing outlasts a weird uneasiness about this whole endeavor, a sense that the things I write and the things I know might be the only things standing between me, the street, and some totally crazy sign. And that the street itself is the only thing standing between humanity and all those impregnable woods. And that I might actually need to earn a master’s degree before these strangers start taking me seriously. I still don’t want to.

*If there are any specific people who believe I am picking on them, the answer is NO!!! Everything is caricature!!!